极小化极大算法保姆级详解

前言

极小化极大算法通常用于完全信息的零和博弈中，即双方的所有信息都是已知的，例如五子棋、象棋。它基于这样一个假设，对方一定会走最利于自己的走法，于是我们在这样的条件下寻找一种最优的策略路径使得己方的收益最大。换句话说，如果在对方最优的走法下我们还能获得优势，则对方走出次优的走法，我们也一定能获得优势。

但需要注意，在这个条件中，对方“最优的走法”是我们认为的“最优的走法”，是否是真实的最优取决于走步生成算法和棋局估值函数。所以极小化极大算法是一种通用的搜索策略路径的算法，在走步生成算法和棋局估值函数完成的前提下，找到最优的策略路径。

博弈树的构建

博弈树的构建是极小化极大算法实现的前提，搜索路径前必须有路才行。简单来说，博弈树构建就一句话，根据当前棋局下棋。如果是己方回合，则用走步生成算法生成一堆可能的走法，然后这些走法再生成一堆对方的走法，实际上就是自己跟自己下棋，走出所有可能的棋局。

当然，所有可能的棋局大部分时候不能穷尽，也许受限于时间，也许受限于空间。这里需要根据游戏规则人为地对走步生成算法做一些优化。同时树的高度也不可能无限高，一直走到已经没棋可下了，通常也需要对树的高度作一个限制，例如自己跟自己最多下10个回合。

以井字棋为例，一个可能的博弈树：

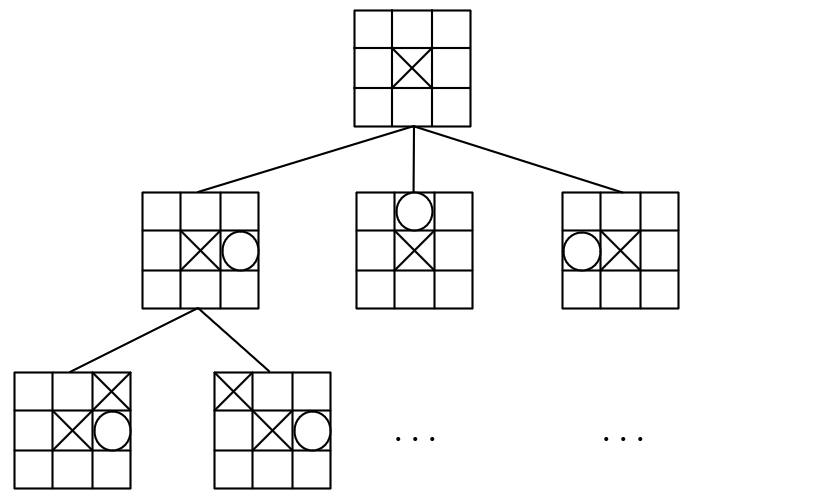
构建完博弈树之后还不够，因为我们不知道哪些走法是最优的，没有一个方法来判断走法的优劣，所以这个时候需要引入棋局评估函数。棋局评估函数就是评估当前棋局对于己方的优劣，给出一个参考的数值，这样就可以比较走法谁好谁坏了。当然，这也是需要人为设计的，棋局评估的准不准也决定着AI的棋力如何。

极小化极大算法过程

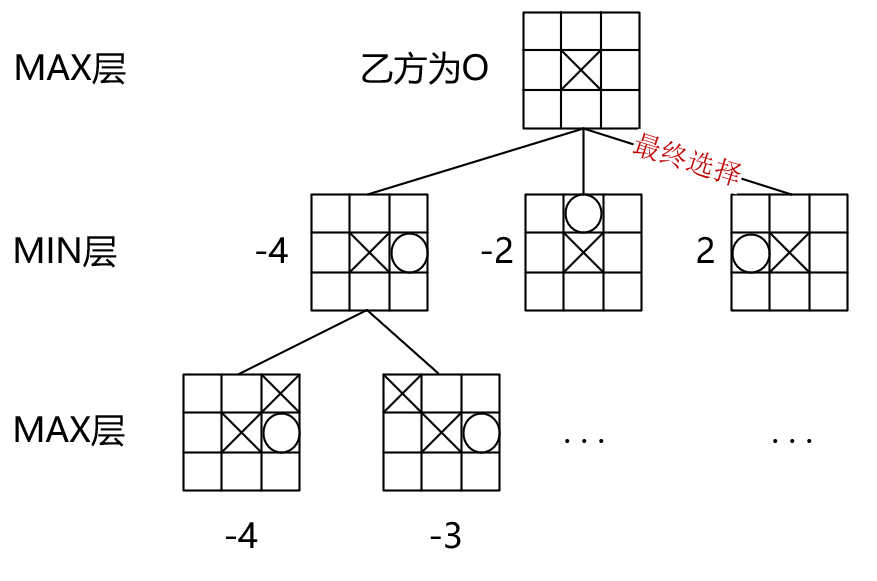
有了以上的博弈树和棋局评估函数，我们就能开始搜索策略路径了，对于博弈树的每一层，我们做一个标识，好让我们知道这时候是谁在下棋。当我们下棋时，就叫做MAX层，这时我们要找到使我们收益最大的走法。当对手下棋时，就叫做MIN层，这时我们要找到使我们收益最小的走法（对方最可能的走法），每个节点都有一个minmax值，作为该节点的预期收益，这是我们最终参考的结果。

对于某一结点minmax值的计算，我们有以下规则：

• 如果是叶节点，其minmax值为棋局评估函数给出的分数
• 如果是在MAX层上，其minmax值为子节点中最大的minmax值（找对我们收益最大的）
• 如果是在MIN层上，其minmax值为子节点中最小的minmax值（找对我们收益最小的）

由上述可以知道，对于非叶节点，其minmax值实际上取决于子节点，所以我们采用自底向上的计算过程计算各节点的预期收益，也就是minmax值。

那么我们就可以总结以上的内容，给出极小化极大算法的过程：

• 首先构建博弈树，这里需要用到走步生成算法
• 然后对叶节点进行棋局评估，计算出minmax值（叶节点可能是无棋可下，也可能是到达了给定的深度，并不一定是在一个深度上）
• 再自底向上计算出非叶节点的minmax值
• 最后，从根节点选择minmax值最大的子节点，作为行动策略。（根节点是MAX层）

一个可能的计算过程，帮助理解：

极小化极大算法并不复杂，但是棋局规模较大的情况下节点数以指数级增加，对空间和时间来说压力都非常大，所以还需要一些剪枝算法进行优化，例如alpha-beta剪枝算法。

你可能也会意识到，上述过程中某些节点没有展开计算的必要，例如MAX层的子节点中已经出现了一个较大的预期收益节点，而其他一些预期收益显然不可能更大的节点，我们就没必要再展开了，这样就可以对博弈树进行剪枝操作，减少开销。本文就不再展开介绍剪枝算法了，alpha-beta剪枝算法日后再详细介绍。

代码实现

minmax核心算法：

int MAX = 0, MIN = 1;

void minmax(NodeTree root, int level){
    if(root->child.size() == 0) return;
    for(int i = 0; i < root->child.size(); i++){
        if(root->child[i]->child.size() != 0){
            minmax(root->child[i], level + 1);
        }
    }
    int result = (level % 2 == 0) ? INT_MIN : INT_MAX;
    for(int i = 0; i < root->child.size(); i++){
        if(level % 2 == MAX){
            if(root->child[i]->val > result){
                result = root->child[i]->val;
            }
        }else if(level % 2 == MIN){
            if(root->child[i]->val < result){
                result = root->child[i]->val;
            }
        }
    }
    root->val = result;
}

博弈树结构和构造如下：

typedef struct Node{
    vector<Node*> child;
    int val;
}*NodeTree;

//  init a tree like this
//  MAX         2
//         /    |   \
//  MIN  -4    -2    2
//       / \   / \  / \
//  MAX -4 -3 -2 1  2 5
NodeTree initTree(){
    NodeTree root = new Node{vector<Node*>(), 0};
    //level2
    Node* b1 = new Node{vector<Node*>(), 0};
    Node* b2 = new Node{vector<Node*>(), 0};
    Node* b3 = new Node{vector<Node*>(), 0};
    root->child.push_back(b1);
    root->child.push_back(b2);
    root->child.push_back(b3);
    //level3
    Node* c1 = new Node{vector<Node*>(), -4};
    Node* c2 = new Node{vector<Node*>(), -3};
    Node* c3 = new Node{vector<Node*>(), -2};
    Node* c4 = new Node{vector<Node*>(), 1};
    Node* c5 = new Node{vector<Node*>(), 2};
    Node* c6 = new Node{vector<Node*>(), 5};
    b1->child.push_back(c1);
    b1->child.push_back(c2);
    b2->child.push_back(c3);
    b2->child.push_back(c4);
    b3->child.push_back(c5);
    b3->child.push_back(c6);

    return root;
}

---