全网最全最易懂的蒙特卡洛树搜索教程！

介绍

之前讲过极小化极大算法和 alpha-beta 剪枝算法，这些是比较简单的决策树和剪枝策略。但是在决策空间比较大的游戏中，例如围棋、象棋，以上算法仍然不能满足，一层就要生成几十个甚至几百个可能的走步，每往下深一层就要指数级递增一次，没多少层就是天文数字了。

即使这个时候有高效的剪枝，在这样的规模面前也无济于事。而现在厉害的 AI，往下推演几十步都是没问题的。这就涉及到更高级的算法了。

蒙特卡洛方法

蒙特卡洛本质上就是一种模拟方法，蒙特卡洛本身其实是摩纳哥的一家赌场，这个名字也代表了这个算法的本质：随机（靠赌）。

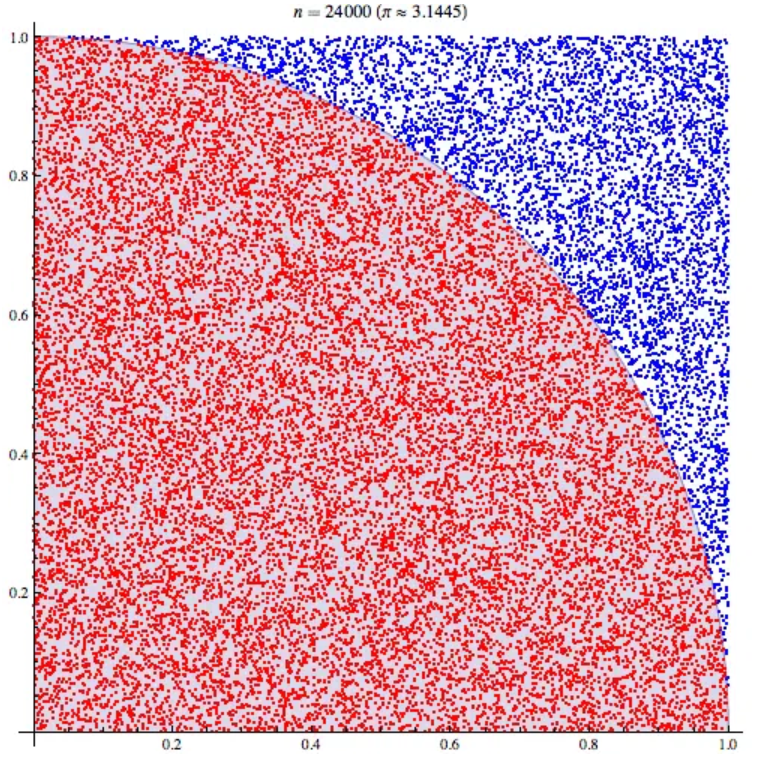
比如想要计算 $\pi$ 的值，我们可以知道圆和矩形面积的对应关系：

$$\frac{圆的面积}{矩形面积}=\frac{\pi r^2/4}{1}=\frac{\pi}{4}$$

然后我们依靠随机落点来求圆的面积，也就是看落在圆内的点有多少个，于是就变成：

$$\frac{圆内点数}{总点数}\approx\frac{\pi r^2/4}{1}=\frac{\pi}{4}$$

点数越多，计算结果越精确。

蒙特卡洛树

回到我们的决策树，在之前的决策树中，具体产生某一步的决策时，需要依赖于先验知识，也就是棋局评估的算法。在生成了一系列可能的走步之后，我们需要依靠棋局评估算法来对节点进行打分，从而最后形成决策。

但是参考蒙特卡洛的思想，我们完全舍弃了先验知识，完全靠随机生成走步来进行探索和决策。

换个角度看，先验知识的上限其实就是人类对游戏决策总结的上限，而蒙特卡洛的上限则是整个决策空间，显然要比人类的上限更高。

从最简单的想法来看，对于当前的局面，我们生成了若干个可能的走步，然后对这每一个走步进行随机模拟。也就是双方随机下棋，直到达到一个终态（游戏结束：赢/输/平局）。每一个走步我们可以进行若干次模拟，最后从概率的角度来看，哪一个走步获胜的概率最高，我们就采取哪个走步。

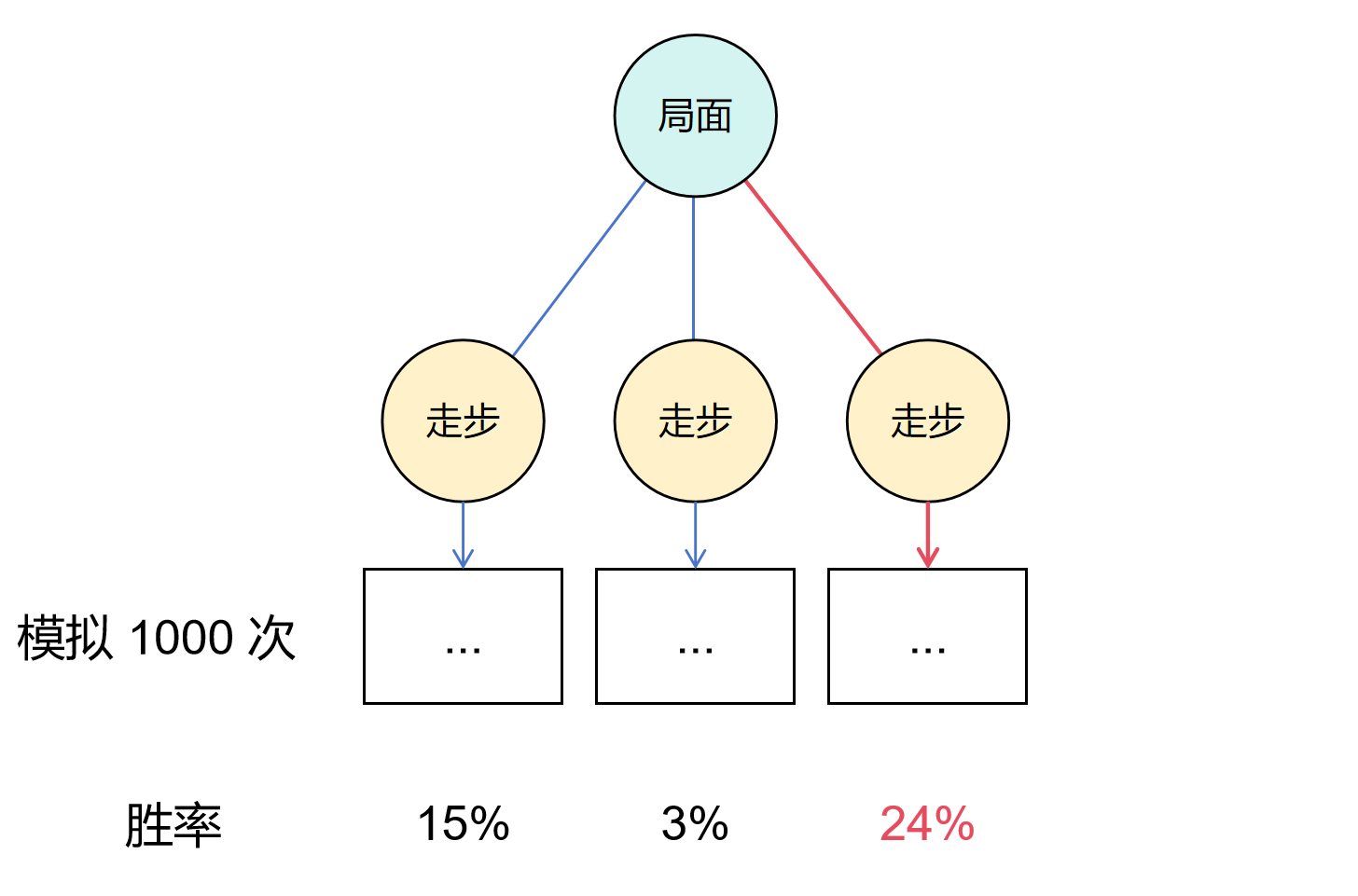
当然上述所说的只是在当前局面下生成了一次走步，这个决策精度是不高的。我们可以继续加深决策树，生成若干轮对局的所有走步，然后对最底层的叶子节点进行模拟，随后采取胜率最高的决策。

但是这样树的规模，其实和极小化极大算法并没有质的区别。

蒙特卡洛树搜索

这种纯随机的方式在各个分支间是完全独立的，也就是每个走步的模拟是独立的，可以并行化。但是缺点也很明显——完全抛弃了先验知识。在生成的走步中，按照经验可以明显判断出哪些走步是显然差的，对于这些走步，其实就没有探索的必要。

所以基于蒙特卡洛树的多种搜索算法就被提出来，让决策本身带有一定的方向，优先探索有潜力的分支，而不是完全依靠随机。

接下来介绍的算法在 2006 年的围棋 AI 中鹤立鸡群，其思路也不算复杂，但是涉及树的算法大多都比较抽象，自己模拟一遍就可以很好的理解了。

核心步骤

在蒙特卡洛树搜索的每一次循环中，会经历以下四个步骤：

1. 选择 Selection：从根节点开始，找到一个最需要拓展的节点，也就是价值最高的子节点
2. 扩展 Expansion：基于当前节点的局面，生成若干个可能的走步
3. 模拟 Simulation：基于当前节点的局面，进行随机走步，直到游戏结束，产生一个结果
4. 反向传播 Backpropagation：将当前节点的结果，沿着父节点向上传递，更新沿途路径的节点信息

其流程图可以表示为：

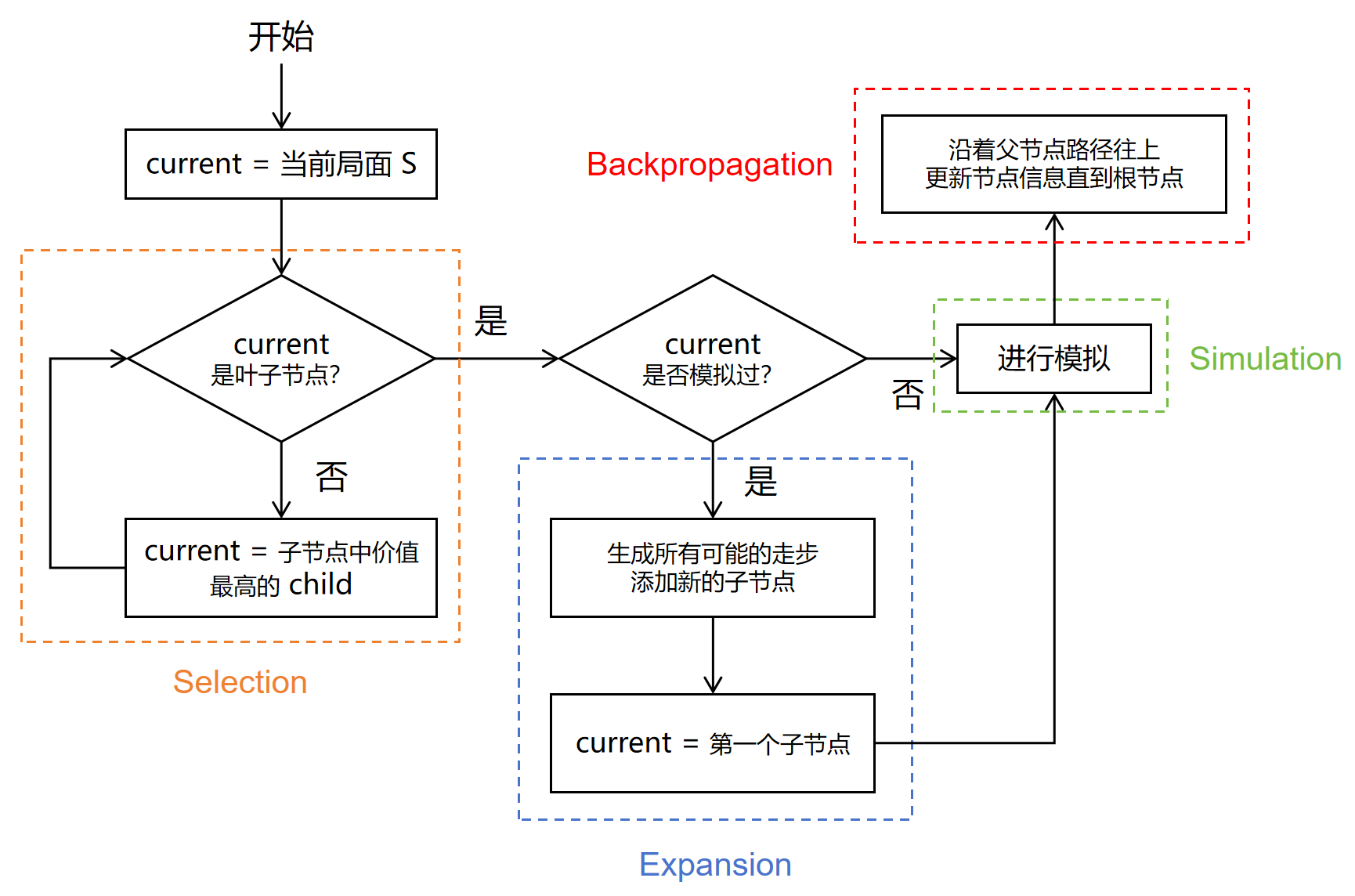
我们现在可以知道大体的算法思路，接下来再具体讲解每一个步骤是如何实现的，以及为什么要这么做。

前置介绍：模拟 Simulation

由于模拟是独立的，不依赖其他步骤，所以我们先讲模拟。

模拟实际上非常简单，就是在当前局面，双方都进行随机的决策，直到游戏结束，产生一个价值。有的游戏结束可能需要非常多步，几百步甚至上千步，这里可以提前截断，然后用估值函数来判断当前残局的价值。

最简单的价值是如果游戏获胜，那么代表当前局面的节点价值就是 1，输了就是 -1，平局就是 0。

这样每个节点都会产生一个价值，以便后续算法进行操作。

1. 选择 Selection

选择的操作实际上是基于模拟的结果，如何判断哪个子节点的价值最高呢？

对于每个节点，他有两个属性，一个是节点的分数值，我们可以用 $t$ 来表示，另一个是节点的模拟次数（包含子节点），我们可以用 $n$ 来表示。

选择基于这样一个公式：$UCB1(S_i)=\bar{V_i} + C\sqrt{\frac{lnN}{n_i}}$

其中 UCB 代表上置信界（Upper Confidence Bound），这个词比较抽象，简单理解就是该节点的潜力有多大。我们对这个公式进行拆解，在一个节点 $i$ 中，$\bar{V_i}$ 代表了这个节点所有模拟的平均价值，换句话说，代表了这个局面及后续局面的平均价值。

而 $C\sqrt{\frac{lnN}{n_i}}$ 这一项代表了一个置信宽度，也就是虽然模拟出来的价值是这样，但是有没有可能有更大的潜力呢。其中 $C$ 是一个常参数，可以根据实际任务进行调整，$N$ 代表了总模拟次数，$n_i$ 代表了这个节点及其子节点的模拟次数。（在实现时一般用节点访问次数来表示）

简单理解这一项就是，模拟次数越少，这一项的值越高，也就是鼓励探索那些没怎么被模拟过的节点，即使当前价值可能比较差，但说不定是潜力股呢。

我们结合流程图来看，假如挑选出来的节点是叶子节点，叶子节点代表当前节点的局面，还没有生成过走步，那么它将会进行下一步扩展。

如果不是叶子节点，那么需要挑选出它最有价值的子节点，然后再回到这一步，直到找到一个叶子节点。

但是为什么会有不是叶子节点的情况呢，这需要结合后续的过程来理解，现在可以暂时保持个疑问。但总之，这是为了保证进行模拟的节点一定是叶子节点。

2. 扩展 Expansion

在前一步选择出最有潜力或价值的节点之后，需要对该节点进行扩展，其实就是生成走步，然后会有代表这些走步的一堆子节点，产生一系列新的局面。这一步除此之外，就没有什么其他的操作了。

3. 模拟 Simulation

需要特别注意的是，要到达第三步，不一定需要经过第二步扩展。思考这样一个初始情况，当前局面生成了三个可能的走步，但是这些走步都没有被模拟过，哪个是最有价值的呢，我该继续扩展哪个局面呢？

无从判断，对吧。但是回到我们的 $C\sqrt{\frac{lnN}{n_i}}$ 这一项，可以注意到此时 $n_i$ 为 0，所以每个节点的价值是正无穷。那么在第一步选择过程中，就必然会选择这些一次都没模拟过的节点，在这种特殊情况下，我们直接进行模拟，就不需要扩展了。

所以再从整体流程理解一下，我们首先需要经历三次的蒙特卡洛树搜索的循环，把这三个可能的走步都模拟一次，这样它的价值才不是正无穷，可以进行比较。然后才会进行扩展，让决策树变深，随后再往更深去探索。

我们结合流程图，如果当前节点是最有价值的节点，而且没模拟过，它价值是正无穷，那显然最有价值，那就模拟。如果最有价值的节点模拟过，代表了它的兄弟节点，也就是其他走步的节点都被模拟过了，这个时候就应该加深去探索，于是就要执行扩展了。你可以反证，如果它的兄弟节点没模拟过，这个节点就不可能是最有价值的。

在扩展完成之后，我们选择第一个子节点进行模拟，从而产生一个结果（价值）。

4. 反向传播 Backpropagation

对于当前叶子节点模拟过后，会产生一个结果，我们简单把结果看作是获胜 1，失败 -1，平局 0。然后就可以沿着父节点往上一直更新信息到根节点。

具体来说，我们先对当前叶子节点自身进行信息更新，比如设置当前节点价值为 1，模拟次数为 1。然后父节点的模拟次数也加 1。不过为了算法的高效性，我们通常会把子节点的价值加到父节点身上，这样方便直接统计所有子节点价值的平均值。

所以实际上可能是这样的，设置当前节点价值为 1，模拟次数为 1；父节点的节点价值加 1，模拟次数也加 1；然后父节点的父节点也需要这样，直到达到根节点。

然后这个时候再从根节点开始下一轮的蒙特卡洛树搜索

步骤总结

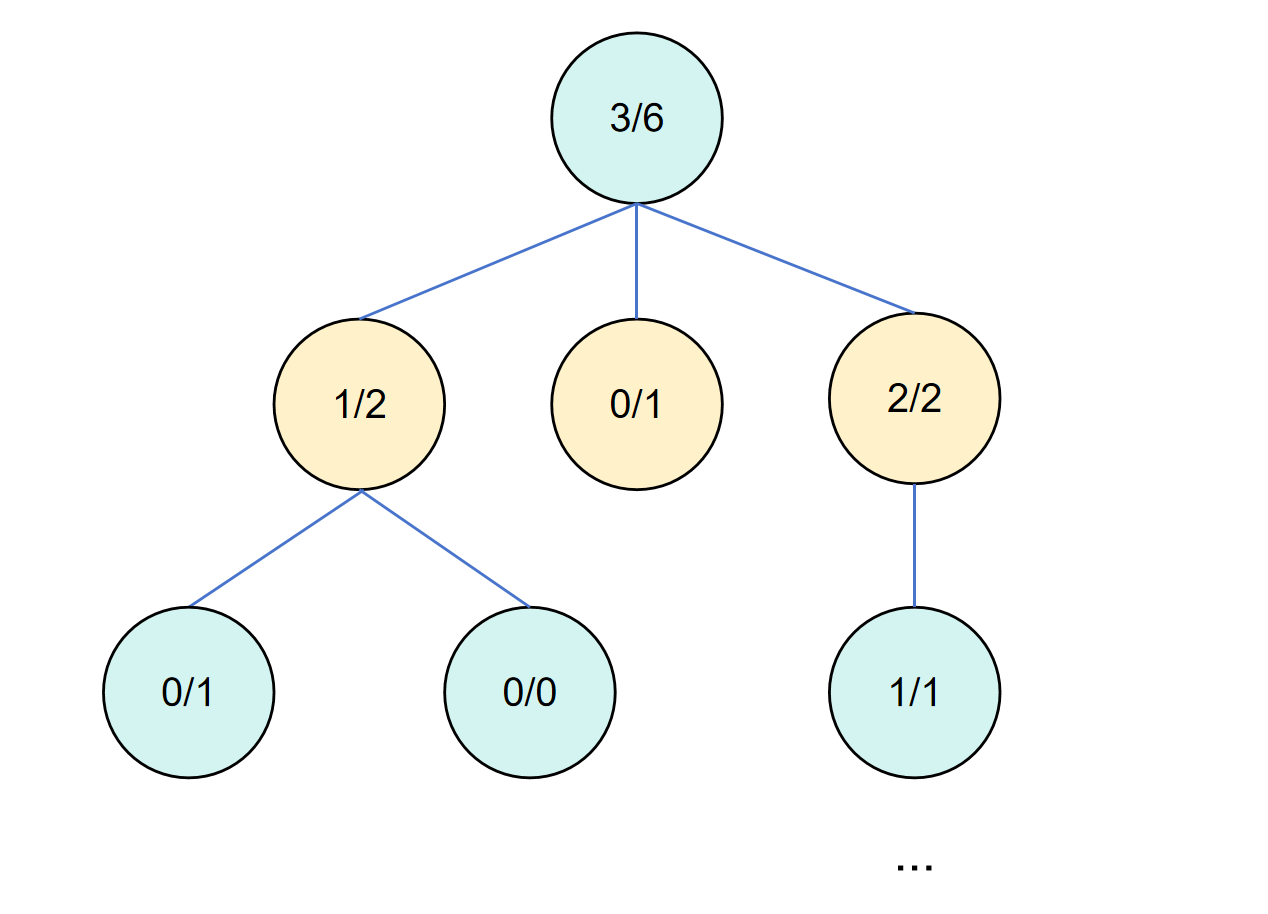
需要注意的是，每一轮（每一次循环）的蒙特卡洛树搜索要经过以上 4 个步骤，当然扩展是非必须的。然后经过一轮轮的迭代循环之后，蒙特卡洛树会逐渐变深，可能会产生这样的一个决策树。

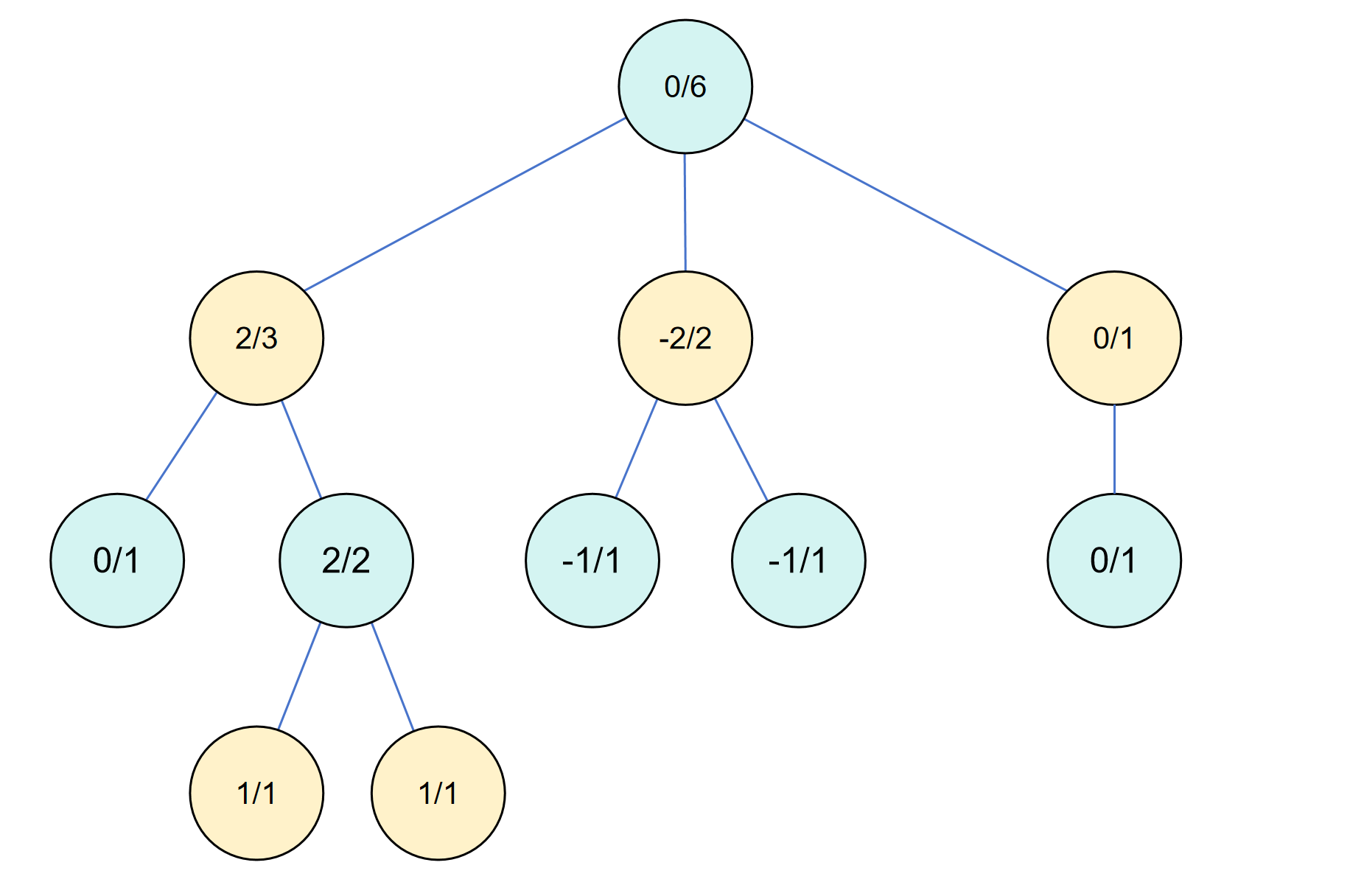
其中节点中的第一个值代表子节点的价值总和，这样除以子节点数就是平均价值，第二个代表该节点的模拟次数。

所以回到第一步的疑问，为什么选择阶段必须要选到一个叶子节点，是因为蒙特卡洛树搜索是要加深决策树，在加深的同时会照顾到那些可能有潜力的分支，也就是没被探索过的。这样经过一轮轮的迭代之后，决策会收敛到一个比较好的分支上，此时我们就选择根节点价值最高的子节点作为我们下一步的决策。

可视化过程

文字上的理解终归是比较抽象的，我们还是通过一个可视化样例来结束这一篇文章，也希望给读者一个比较直观的理解。这里为了简单，模拟结果只有输（0）和赢（1）。

第一轮循环

对于初始根节点，我们可以特殊处理，让他不走算法的流程。也可以一视同仁，把他视作是一个叶子节点，进行一次模拟，不过此时的模拟意义并不大（影响也不大），但是对所有节点进行统一处理在实现上更优雅一些。

为了代码的优雅，我们把他当做叶节点，进行一次模拟。

假设模拟结果是输，此时模拟次数是 1，分数是 0。

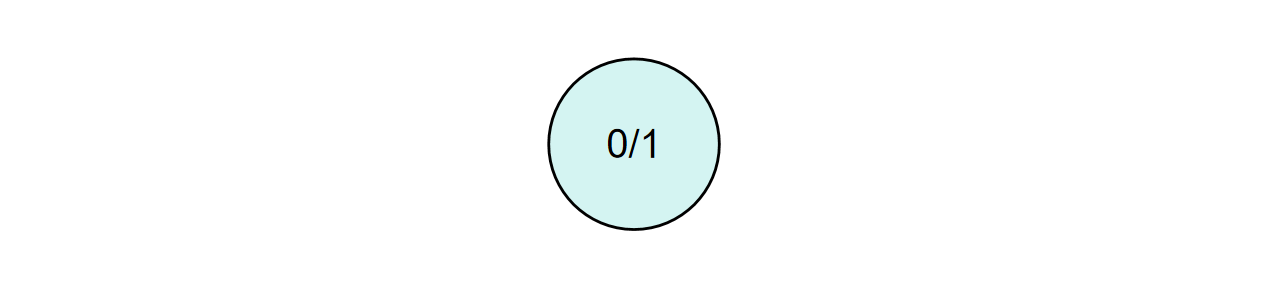
随后我们反向传播，由于没有父节点，所以反向传播不会执行任何操作。

第二轮循环

下一轮循环再次从根节点出发，此时我们模拟过了根节点，所以要进行拓展的操作，假设拓展出三个子节点。

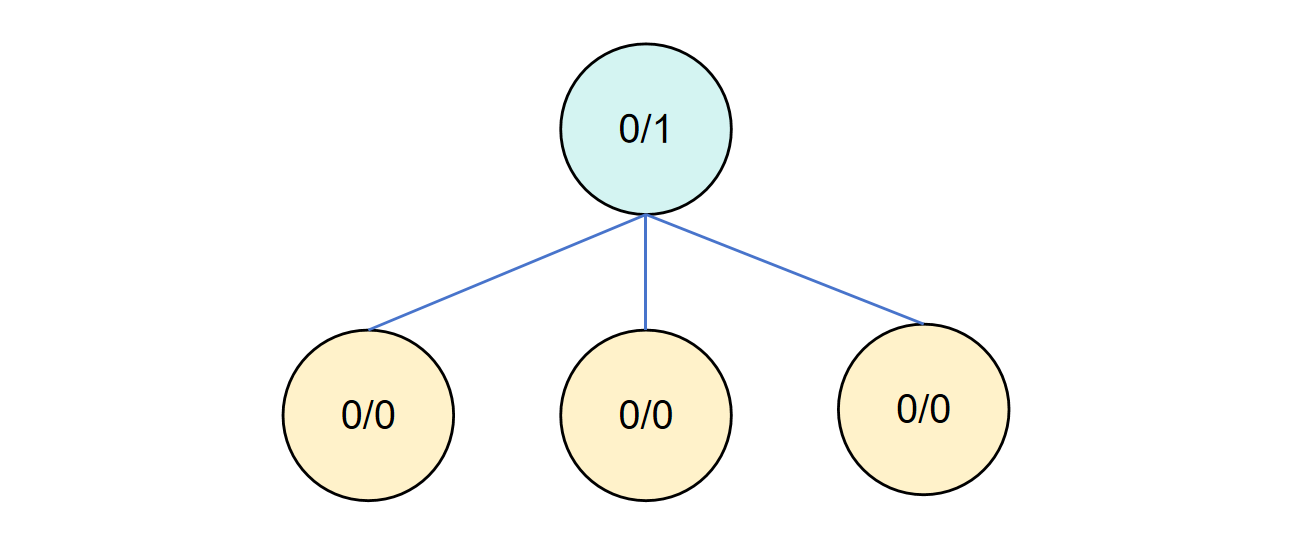
在拓展之后对第一个子节点进行模拟，假设结果是赢，并进行反向传播更新父节点。

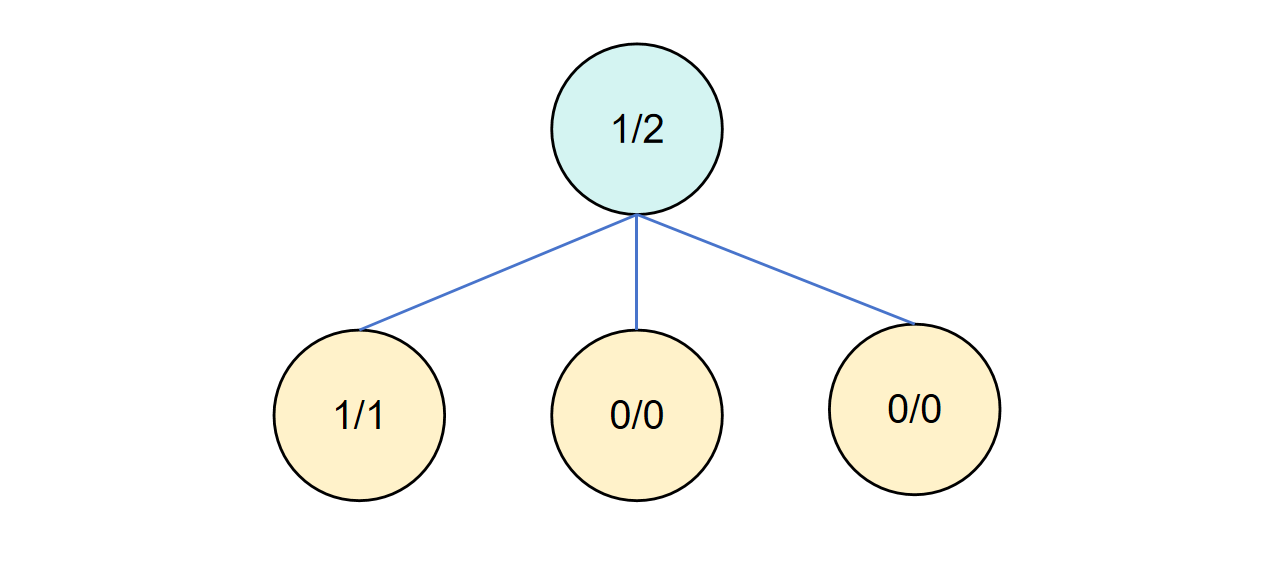
随后回到根节点进行下一轮循环。

第三轮循环

此时第二个子节点没有模拟过，所以其 UCB 值是无穷大，我们需要模拟该节点，并进行反向传播。

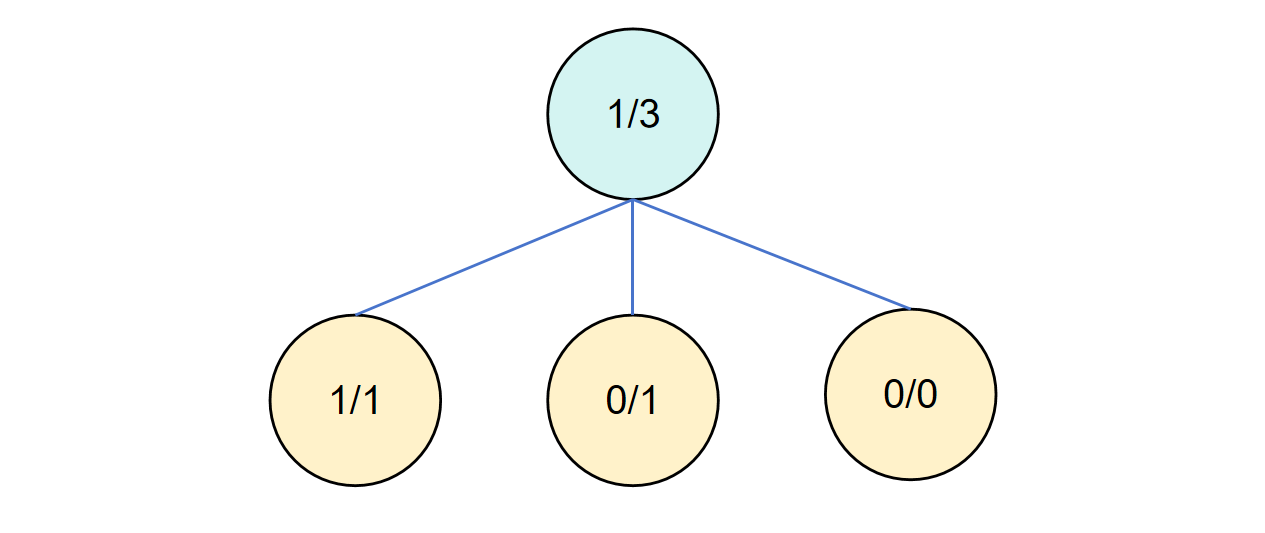
第四轮循环

同上。

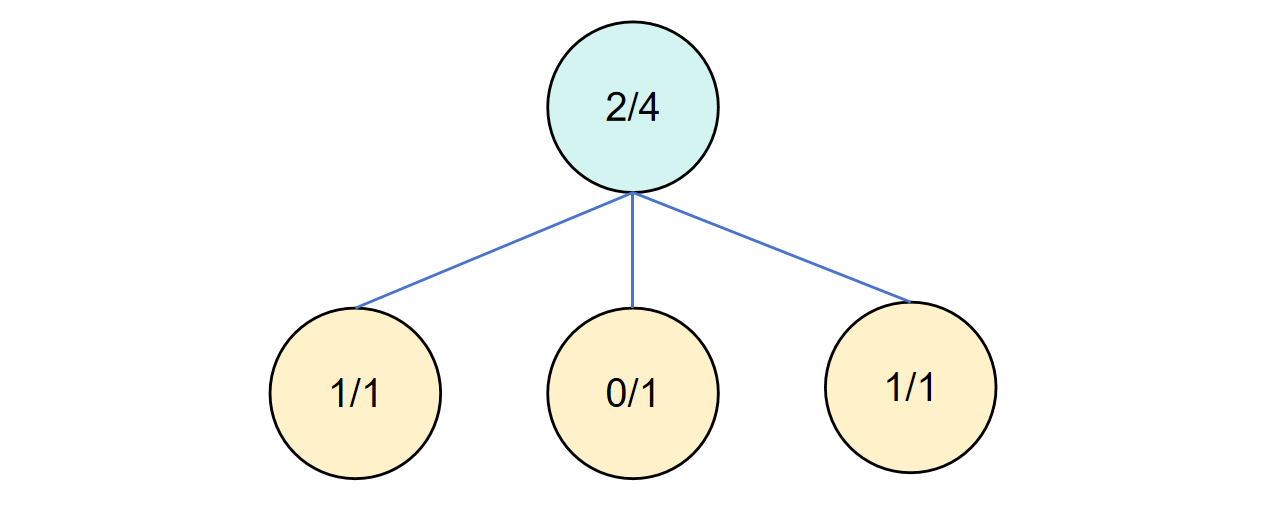
第五轮循环

此时在选择阶段，第一个子节点和第三个子节点价值一样，我们可以选第一个进行拓展。

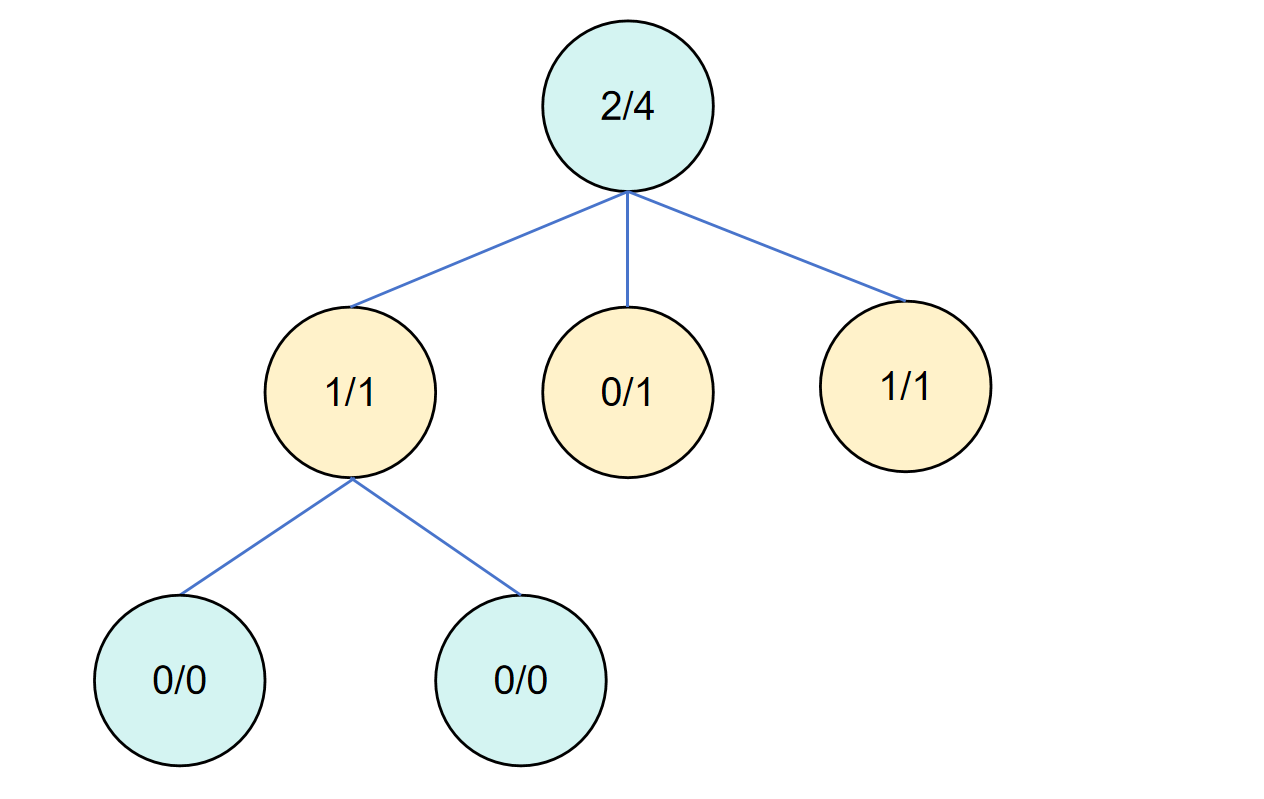
拓展完成后对第一个子节点进行模拟，并反向传播。

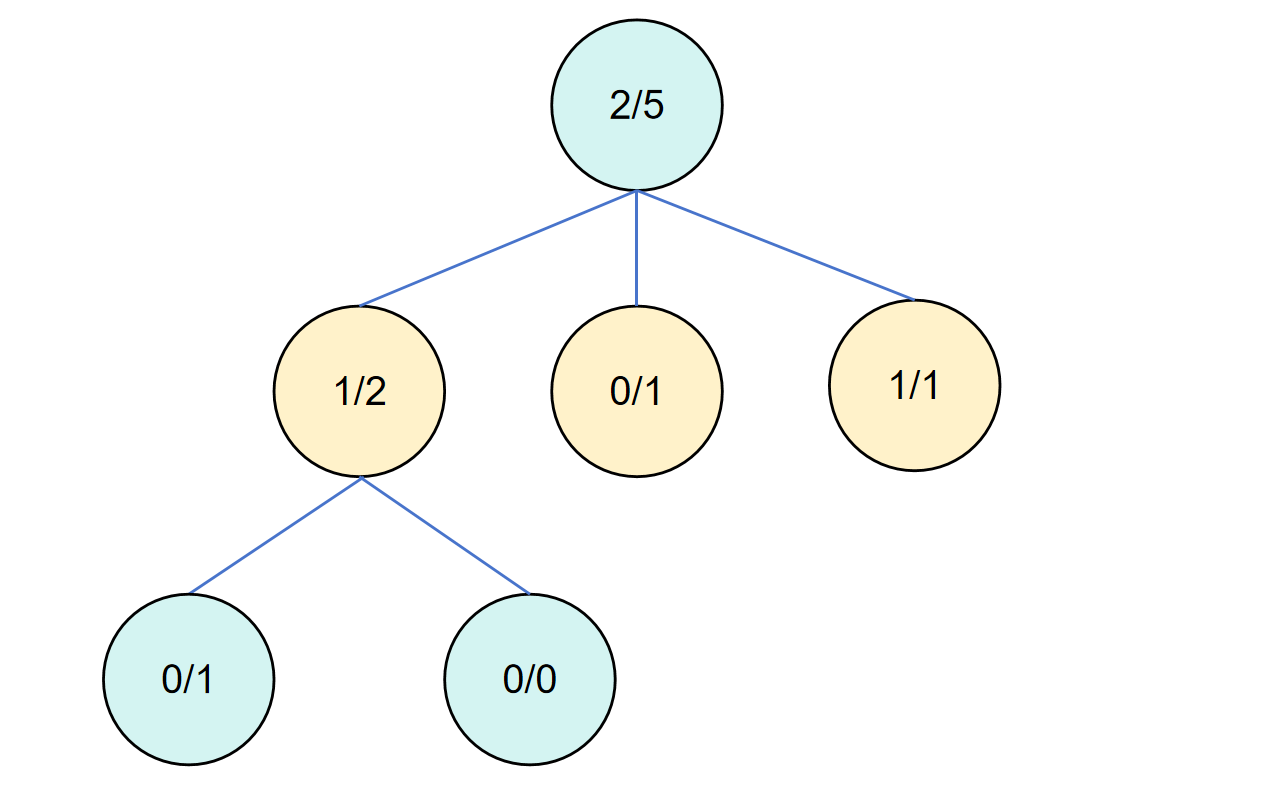
第六轮循环

此时从根节点出发选择子节点，发现第三个子节点价值更高，对第三个子节点进行拓展。

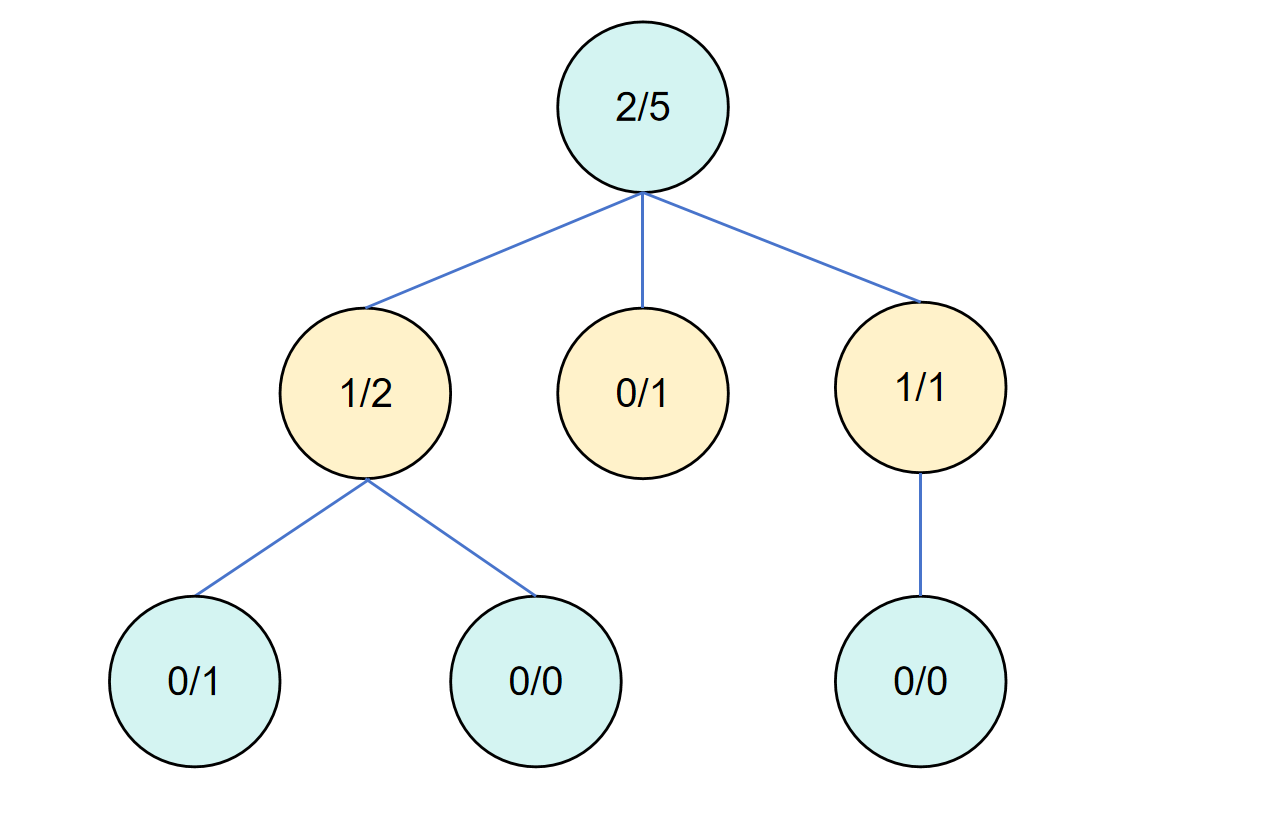
随后对第三个子节点的子节点进行模拟，并反向传播。

此时由于第三个子节点价值最高，后续还会对该子节点进行加深和探索。

Python 代码实现

为了实现一个可用性比较好的代码框架，我们可以对这个算法提取出抽象的部分，也就是节点定义和算法流程这部分对所有蒙特卡洛树搜索是一致的。不一致的只有模拟这部分，所以我们就可以实现一个抽象层的接口。

不过为了简洁性，本文的代码删去了保证程序健壮的非法检查和会导致理解成本上升的优化方法。有感兴趣优化代码性能的可以自行实验。

蒙特卡洛树节点定义

我们把蒙特卡洛树搜索的单个步骤都写到节点的方法中，只有扩展和模拟是根据不同的场景定义的，需要用户自己编写。

在实现中需要特别注意节点的终结状态，无法再拓展出新的局面了，实际上就是游戏已经结束了。

另外，还需要额外区分游戏是否是零和博弈，在零和博弈中，我方的决策应该采用对我方价值最大的，但是对方的决策应该采取对我方价值最小的，以满足对方也很聪明的假设。否则我们会找到对方以最笨的方式让我们最快胜利的路径，因为此时价值是最大的。其实就是 Minmax 算法。

在具体实现中，我们参考 Negamax 算法，本质上是 Minmax 算法的数学优化形式，基于对称性，通过统一的递归结构简化。

对称性简单理解就是，对于 A 最优的局面，对于 B 就是最差的。假设价值为 S，如果取负，那么 B 要挑选对他最有利的局面，就是取 S 中的最大值。因为从绝对值来看是最小的，也就是对 A 最不利。视角翻转，对 A 的选择来说也是一样的。

这样所有节点对于价值的判断就一致了，只要取最大值就可以了。在实现中，只要每一层的价值取反，这样往上传播就可以理解成角色互换，每一层都是在选取对自己最有利的局面。具体的数学证明可以看相关的文献，就不再赘述了。

具体实现中，我们只需要在 backpropagate() 函数中，往上递归的过程加个负号就行了，非常优雅。

class MonteCarloTreeNode(ABC):
    exploration_weight: float = 1.0

    def __init__(self, minmax_search: bool = True):
        self.visit = 0
        self.score = 0
        self.children = []
        self.is_terminal = False
        self.parent: MonteCarloTreeNode = None
        self.minmax_search = minmax_search

    @abstractmethod
    def expand(self) -> list["MonteCarloTreeNode"]:
        raise NotImplementedError("expand")

    @abstractmethod
    def simulate(self) -> float:
        raise NotImplementedError("simulate")

    def expand_node(self) -> None:
        self.children = self.expand()
        if len(self.children) == 0:
            self.is_terminal = True
            return

        for child in self.children:
            child.parent = self

    def backpropagate(self, result: float) -> None:
        self.visit += 1
        self.score += result
        if self.parent is not None:
            self.parent.backpropagate(-result if self.minmax_search else result)

    def select(self, N: int) -> "MonteCarloTreeNode":
        if len(self.children) == 0:
            return self

        best_child = self.children[0]
        best_ucb1 = best_child.ucb1(N)

        for child in self.children:
            if child.visit == 0:
                return child
            ucb1 = child.ucb1(N)
            if ucb1 > best_ucb1:
                best_ucb1 = ucb1
                best_child = child

        return best_child

    def ucb1(self, N: int) -> float:
        if self.visit == 0:
            return float('inf')
        return (self.score / self.visit) + MonteCarloTreeNode.exploration_weight * (math.log(N) / self.visit)

蒙特卡洛树定义

这部分比起节点就简单多了，只需要把流程串起来就可以了。在选择最优落子的逻辑中，我们采取的是选访问次数最多的节点，为什么不是 UCB 值或者平均价值呢？

UCB 值代表的是这个分支的「潜力」，并非他的价值。直观理解就是他可能有价值，但是可能探索几次之后发现不太行，那之后就不再探索了。还记得不，探索次数越少，UCB 值越高。

而平均价值代表的是所有子节点的平均价值，可能有的局面存在「神之一手」，只有这一步价值非常高，而其他节点价值都非常低，那么看平均价值也是不合理的。

访问次数多代表这个节点被探索的程度高，也就是他好不好，我们对他的置信程度是比较高的，是一个比较稳的选择。另一方面，访问次数多，也代表这个节点的潜力大，UCB 值高才会一直访问这个节点。在访问次数高的同时，UCB 值还大，那就只能说明这个节点的价值要比其他节点高。所以这样的选择是合理的。

class MonteCarloTree(ABC):
    def __init__(self, root: MonteCarloTreeNode):
        self.root = root

    def search(self, iterations: int = None) -> MonteCarloTreeNode:
        def search_iter(curr: MonteCarloTreeNode) -> MonteCarloTreeNode:
            while len(curr.children) > 0:
                curr = curr.select(self.root.visit)
            if not curr.is_terminal and curr.visit != 0:
                curr.expand_node()
                if not curr.is_terminal:
                    curr = curr.children[0]
            score = curr.simulate()
            curr.backpropagate(score)
            return curr

		for _ in range(iterations):
			search_iter(self.root)

        best_child = self.root.children[0]
        for child in self.root.children[1:]:
            if child.visit > best_child.visit:
                best_child = child

        return best_child

蒙特卡洛树可视化

其中为了方便理解和 debug，我还实现了决策树的可视化，依赖 graphviz，需要自行安装其二进制可执行文件到系统中。（https://graphviz.org/download/）

from graphviz import Digraph

class TreeDrawer():
    def __init__(self):
        self.frame = 0

    def draw(self, tree, filename: str = "mcts_tree") -> None:
        dot = Digraph(comment='Monte Carlo Tree')
        dot.attr('node', shape='box', style='filled', fillcolor='lightblue')
        dot.attr('edge', fontsize='10')

        # Mark the select route
        curr = tree.root
        select_route = []
        while len(curr.children) > 0:
            curr = curr.select(tree.root.visit)
            select_route.append(curr)

        # Add nodes recursively
        def add_nodes(node: MonteCarloTreeNode) -> None:
            label = f"Visits: {node.visit}\nScore: {node.score:.2f}"
            if node.visit > 0:
                label += f"\nAvg: {node.score/node.visit:.2f}"

            node_id = str(id(node))
            dot.node(node_id, label)

            if node is tree.root:
                # Root node style
                dot.node(node_id, label, style='filled', fillcolor='gold')
            elif node.is_terminal:
                # Terminal node style
                dot.node(node_id, label, style='filled', fillcolor='salmon')
            elif node in select_route:
                # Selected node style
                dot.node(node_id, label, style='filled', fillcolor='lightgreen')

            for child in node.children:
                child_id = str(id(child))
                ucb1 = "INF" if child.visit == 0 else f"{child.ucb1(node.visit):.4f}"
                dot.edge(node_id, child_id, label=ucb1)
                add_nodes(child)
        add_nodes(tree.root)

        dot.graph_attr['dpi'] = str(300)
        dot.format = 'png'
        dot.render(f"{filename}_{self.frame}", view=False, cleanup=True)
        print(f"Save {filename}_{self.frame}.png")
        self.frame += 1

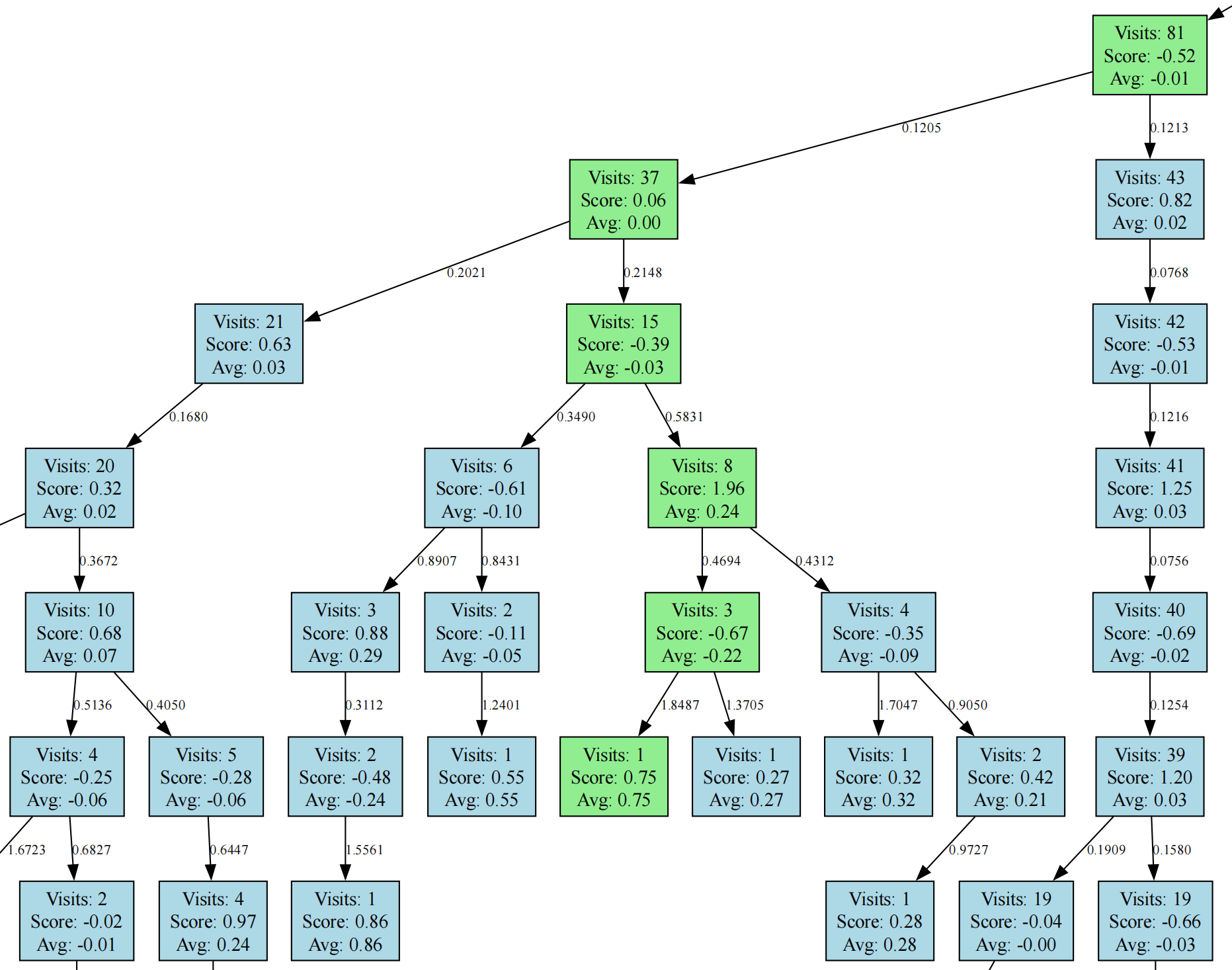
我们可以看一个可视化的示例来感受一下决策树，图中标绿的就是 select 的选择路径。

同时我还在边上标注了 UCB 值，可以很直观的对树进行可视化和 Debug。

蒙特卡洛树-井字棋实战

为了验证蒙特卡洛树，这里简单实现了一个井字棋的游戏，同时对可视化做了井字棋的局面展示，有兴趣的可以在我的 github 主页上查看，代码太长就不放在这里了。

https://github.com/Syan-Lin/pyMCTS

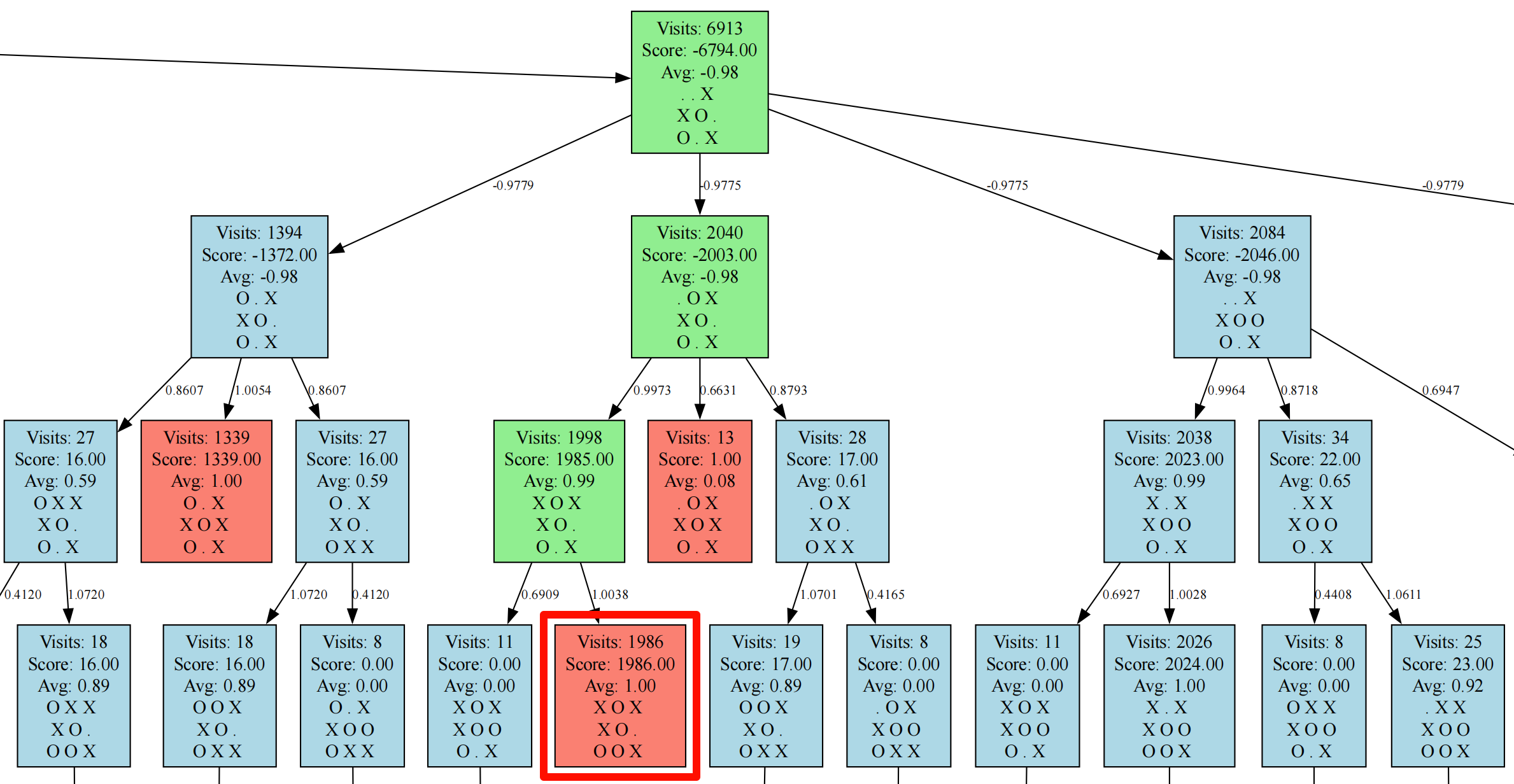
从可视化的结果可以看出，决策树似乎困在这个输的终态非常久，如果要进一步优化的话，对于已经输的终态局面，可以返回一个很大的负值进行传播，从而避免一直困在这里搜索。

最后探究一下我们实现的 AI 棋力如何，其实在蒙特卡洛树中，棋力基本只和搜索的深度有关。在搜索迭代次数为 100 时，我模拟了 1,000 局同棋力的 AI 对局，先手的有 54% 的胜率，9.9% 的平局率和 36.1% 的败率。可以说这个棋力略高于随机下棋。

随后尝试了不同迭代次数，均模拟 1,000 局，最终结果如下表：

迭代次数	胜场	平局	败场
100	540	99	361
1000	778	139	83
10000	732	240	37
100000	33	967	0

在 10,000 次之前，先手都是有巨大优势的，当迭代次数上升至 100,000 时，基本已经可以穷尽这个游戏的决策空间了，在 AI 和 AI 的对战中，几乎每局都是平局。

---