力扣 407 接雨水 II

题目描述

给你一个 m x n 的矩阵，其中的值均为非负整数，代表二维高度图每个单元的高度，请计算图中形状最多能接多少体积的雨水。

示例 1：

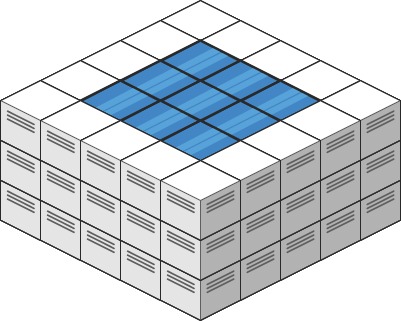
输入: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]
输出: 4
解释: 下雨后，雨水将会被上图蓝色的方块中。总的接雨水量为1+2+1=4。

示例 2：

输入: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]]
输出: 10

提示:

• m == heightMap.length
• n == heightMap[i].length
• 1 <= m, n <= 200
• 0 <= heightMap[i][j] <= 2 * 104

解题思路

相比一维的接雨水，只需要考虑一个维度的高度，对于当前的格子，能装多少水取决于左边和右边的最大高度。在二维空间中，不仅需要考虑左右，还需要考虑上下，而且不能仅仅考虑最大高度，还需要考虑包围性，这就导致问题的复杂性一下上升了一个维度。

但是我们可以将问题进行拆解，考虑一个最简单的规模，即周围四个格子（上下左右）的高度是确定的，那么该格所能接的水取决于周围四个格子最短的那一个。简单说就是木桶效应，最短的格子决定了能装多少水。那能不能把问题简化成四个格子呢？

首先我们考虑一个较大的范围，从宏观角度上，将整个二维空间视作一个木桶，那么能装多少水取决于最外层的格子高度，例如示例二的图。另外，我们可以确定，一个水域内水的高度一定是相等的，而且取决于所围成木桶最短的那个格子。

基于这样的考虑，我们可以做一个简化，假设一个格子所接的水的高度是可以确定的，那么此时它就可以被视为是一个木板，可以负责「包围」其他格子里的水。

有这样的简化操作之后再回到宏观，可以确定的是，最外围最短的那个格子，一定可以决定内部所能装水的「下限」，在所有可能的情况下，至少都能装最外围最短格子高度的水，水高了可能漏出去，但是低了绝对不可能漏出去，最低的木板已经确定了。

所以我们从最外层最短的那个格子出发，然后查看周围非木板格子是否可以装水，那么这样就会有两种情况：

1. 最短那个格子周围可以装水，那么此时就可以确定装水量，并将该格视为是「木桶的木板」。
2. 最短那块木板周围不能装水，也就是周围存在比外围最短格子还高的，那么此时就可以把这个格子当作是「木桶的木板」。（参考图 1 中的边缘非常短的格子）

需要注意的是周围这个概念，由于我们是从最外层的格子开始，所以周围是只能向内部进行的。也就是说，随着不断确定周围的格子，宏观上来看，是逐渐从外部向内确定每个格子所能装的水。

由于我们将确定的范围缩小至一个相邻（上下左右），所以可以很好地确定能装的水最多是多少，肯定不可能超过当前这块「木桶的木板」的高度，那有没有可能更低呢？也不可能，因为我们挑选的这块木板是最短的，最少也能装这个高度的水，所以也不可能更低，于是就可以确定这个格子周围所能装的水。

所以这个算法的过程就是，先取最外围的网格，挑选出最矮的那一个，然后查看周围非木板格子，确定一个新的「木板」，有可能可以装水，也有可能不行，但最后都会被视为是新的「木板」。然后把这个新的「木板」当作是围成木桶的「木板」，再去寻找下一个最短的，确定其周围的格子所能装的水。这样循环往复，当所有格子都成为「木板」之后，所能装的水就都计算完了。（可视化过程）

那么为了高效地获得这个最短的木板，我们就需要一个最小堆。为了记录谁是木板，就需要一个 visit 数组，所以最后代码如下：

class Solution {
public:
    int trapRainWater(vector<vector<int>>& heightMap) {
        using pos = pair<int, int>;

        int m = heightMap.size(), n = heightMap[0].size();
        if (m <= 2 || n <= 2) {
            return 0;
        }

        int result = 0;
        // 用来记录围成木桶的木板
        vector<vector<int>> visited(m, vector<int>(n, 0));
        // 需要记录最短木板的长度和坐标
        priority_queue<pair<int, pos>, vector<pair<int, pos>>, greater<pair<int, pos>>> minHeap;

		// 初始围成木桶的木板是最外围
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(i == 0 || i == m - 1 || j == 0 || j == n - 1) {
                    minHeap.push({heightMap[i][j], {i, j}});
                    visited[i][j] = 1;
                }
            }
        }

		// 一种常见的上下左右偏移操作
        array<int, 5> dirs = {-1, 0, 1, 0, -1};
        while(!minHeap.empty()) {
            auto [height, pos] = minHeap.top();
            minHeap.pop();
            for(int i = 0; i < dirs.size() - 1; i++) {
                int x = pos.first + dirs[i];
                int y = pos.second + dirs[i + 1];

                if(x >= 0 && x < m && y >= 0 && y < n && !visited[x][y]) {
                    if(height > heightMap[x][y])
                        result += height - heightMap[x][y];
                    minHeap.push({max(heightMap[x][y], height), {x, y}});
                    visited[x][y] = 1;
                }
            }
        }

        return result;
    }
};