力扣题解：135. 长度最小的子数组（困难）

题目

n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。

你需要按照以下要求，给这些孩子分发糖果：

• 每个孩子至少分配到 1 个糖果。
• 相邻两个孩子评分更高的孩子会获得更多的糖果。

请你给每个孩子分发糖果，计算并返回需要准备的 最少糖果数目 。

示例 1：

输入：ratings = [1,0,2]
输出：5
解释：你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。

示例 2：

输入：ratings = [1,2,2]
输出：4
解释：你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。
     第三个孩子只得到 1 颗糖果，这满足题面中的两个条件。

提示：

• n == ratings.length
• 1 <= n <= 2 * 10^4
• 0 <= ratings[i] <= 2 * 10^4

思路：我们首先有一个最朴素的想法，为了让总糖果数最小，如果下一个孩子得分更高，那无论他分多高，都只多分一个。那么我们就得到一个处理升序序列的方法。

从左向右遍历，可以得到数组的升序关系，有以下规则：

• 当右边的孩子评分更高时，他得到的糖果比左边多一个
• 否则，他只分到一个糖果

第一次遍历过后，我们已经处理完整个数组的升序序列，如下图所示，那么就还剩下降序序列需要处理。

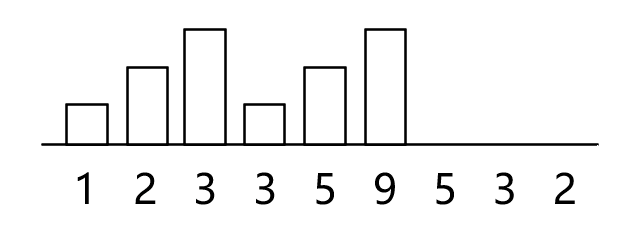
对于降序我们不好直接处理，如果右边的孩子得分比左边低，让他的糖果比左边的少一个，那么如果降序序列过长，可能导致糖果数量小于0，又或者右边已经是降序序列的最后一个元素，可以直接设为1。
所以从降序方向上，并不好判断到底该分几个糖果，因为糖果有一个下界，从降序的方向上有可能突破下界。

但是从另外一个角度思考，一个方向上的降序序列就是另一个方向的升序序列，所以我们从右向左遍历，处理数组的降序序列。

从右向左遍历，可以得到数组的降序关系，有以下规则：

• 当左边的孩子评分更高时，他得到的糖果比右边多一个
• 否则，他只分到一个糖果

但是这两种遍历方法显然会出现冲突，例如下图。出现这种情况是因为9这个元素是峰值，要满足[3,5,9]升序的最小值是3，而满足[9,5,3,2]降序的最小值是4，那显然9这个元素糖果最少是4，取多的那一个。

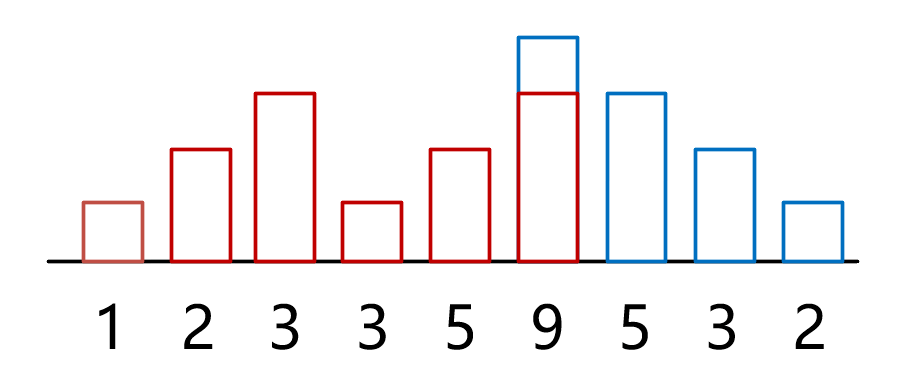
所以我们有一个最后的调整规则：result[i] = max(left[i], right[i])（left 为从左向右遍历的结果，right 为从右向左遍历的结果，result 为最终结果）

另外，本题空间复杂度还可以继续压缩至常数级别，感兴趣可以继续阅读官方题解。

题解：

• 时间复杂度：O(n)
• 空间复杂度：O(n)

class Solution {
public:
    int candy(vector<int>& ratings) {
        vector<int> left(ratings.size(), 1);
        for(int i = 0; i < ratings.size(); i++){
            if(i > 0 && ratings[i] > ratings[i - 1]){
                left[i] = left[i - 1] + 1;
            }
        }

        vector<int> right(ratings.size(), 1);
        for(int i = ratings.size() - 1; i >= 0; i--){
            if(i < ratings.size() - 1 && ratings[i] > ratings[i + 1]){
                right[i] = right[i + 1] + 1;
            }
        }
        int result = 0;
        for(int i = 0; i < ratings.size(); i++){
            result += max(left[i], right[i]);
        }
        return result;
    }
};

---